Distributionally Robust Predictive Runtime Verification under Spatio-Temporal Logic Specifications

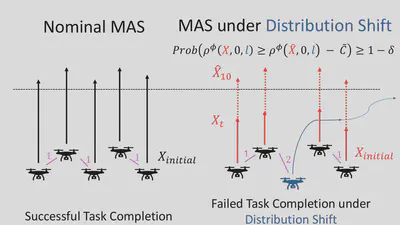
Cyber-physical systems designed in simulators, often consisting of multiple interacting agents, behave differently in the real-world. We would like to verify these systems during runtime when they are deployed. Thus, we propose robust predictive runtime verification (RPRV) algorithms for (1) general stochastic CPS under signal temporal logic (STL) tasks, and (2) stochastic multi-agent systems (MAS) under spatio-temporal logic tasks. The RPRV problem presents the following challenges (1) there may not be sufficient data on the behavior of the deployed CPS, (2) predictive models based on design phase system trajectories may encounter distribution shift during real-world deployment, and (3) the algorithms need to scale to the complexity of MAS and be applicable to spatio-temporal logic tasks. To address these challenges, we assume knowledge of an upper bound on the statistical distance (in terms of an f-divergence) between the trajectory distributions of the system at deployment and design time. We are motivated by our prior work [1, 2] where we proposed an accurate and an interpretable RPRV algorithm for general CPS, which we here extend to the MAS setting and spatio-temporal logic tasks. Specifically, we use a learned predictive model to estimate the system behavior at runtime and robust conformal prediction to obtain probabilistic guarantees by accounting for distribution shifts. Building on [1], we perform robust conformal prediction over the robust semantics of spatio-temporal reach and escape logic (STREL) to obtain centralized RPRV algorithms for MAS. We empirically validate our results in a drone swarm simulator, where we show the scalability of our RPRV algorithms to MAS and analyze the impact of different trajectory predictors on the verification result. To the best of our knowledge, these are the first statistically valid algorithms for MAS under distribution shift.